将偏差的比例(Proportion)、积分(Integral)和微分(Differential)通过线性组合构成控制量,用这一控制量对被控对象进行控制,这样的控制器称PID控制器。在社区开源的CW32L011无刷电机驱动器有感控制代码就用到了相关方法。也是电机控制必备知识。
1模拟PID控制原理
在模拟控制系统中,控制器最常用的控制规律是PID控制。为了说明控制器的工作原理,先看一个例子。如图1所示是一个小功率直流电机的调速原理图。给定速度n0(t)与实际转速进行比较,其差值e(t)=n0(t)-n(t),经过PID控制器调整后输出电压控制信号u(t),u(t)经过功率放大后,驱动直流电动机改变其转速。
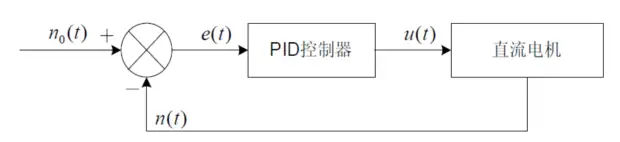
图1 小功率直流电机调速系统
常规的模拟PID控制系统原理框图如图2所示。该系统由模拟PID控制器和被控对象组成。图中,r(t)是给定值,y(t)是系统的实际输出值,给定值与实际输出值构成控制偏差e(t),所以:
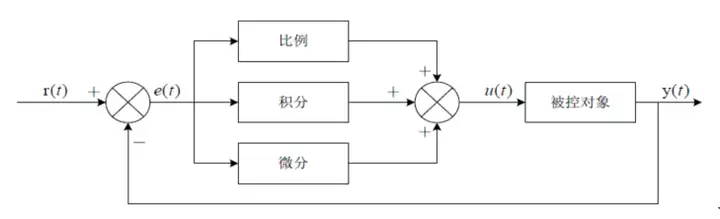
图2 模拟PID控制系统原理图
e(t)作为PID控制的输入,u(t)作为PID控制器的输出和被控对象的输入。所以模拟PID控制器的控制规律为:
其中:Kp为控制器的比例系数;Ti为控制器的积分时间,也称积分系数;Td为控制器的微分时间,也称微分系数。
1).比例部分
比例部分的数学式表示是:Kp* e(t)。
在模拟PID控制器中,比例环节的作用是对偏差瞬间作出反应。偏差一旦产生控制器立即产生控制作用,使控制量向减少偏差的方向变化。控制作用的强弱取决于比例系数,比例系数越大,控制作用越强,则过渡过程越快,控制过程的静态偏差也就越小;但是越大,也越容易产生振荡,破坏系统的稳定性。故而,比例系数选择必须恰当,才能过渡时间少,静差小而又稳定的效果。
2).积分部分
积分部分的数学式表示是:
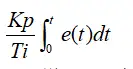
从积分部分的数学表达式可以知道,只要存在偏差,则它的控制作用就不断的增加;只有在偏差为零时,它的积分才能是一个常数,控制作用才是一个不会增加的常数。可见,积分部分可以消除系统的偏差。
积分环节的调节作用虽然会消除静态误差,但也会降低系统的响应速度,增加系统的超调量。积分常数越大,积分的积累作用越弱,这时系统在过渡时不会产生振荡;但是增大积分常数会减慢静态误差的消除过程,消除偏差所需的时间也较长,但可以减少超调量,提高系统的稳定性。当积分常数较小时,则积分的作用较强,这时系统过渡时间中有可能产生振荡,不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定积分系统。
3).微分部分
微分部分的数学式表示是:
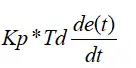
实际的控制系统除了希望消除静态误差外,还要求加快调节过程。在偏差出现的瞬间,或在偏差变化的瞬间,不但要对偏差量做出立即响应(比例环节的作用),而且要根据偏差的变化趋势预先给出适当的纠正。为了实现这一作用,可在PI控制器的基础上加入微分环节,形成PID控制器。
微分环节的作用是阻止偏差的变化。它是根据偏差的变化趋势(变化速度)进行控制。偏差变化的越快,微分控制器的输出就越大,并能在偏差值变大之前进行修正。微分作用的引入,将有助于减小超调量,克服振荡,使系统趋于稳定,特别对髙阶系统非常有利,它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感,对那些噪声较大的系统一般不用微分,或在微分起作用之前先对输入信号进行滤波。
微分部分的作用由微分时间常数决定。微分系统越大时,则它抑制偏差变化的作用越强;越小时,则它反抗偏差变化的作用越弱。微分部分显然对系统稳定有很大的作用。
适当地选择微分常数,可以使微分作用达到最优。
由于计算机的出现,计算机进入了控制领域。人们将模拟PID控制规律引入到计算机中来。对式2的PID控制规律进行适当的变换,就可以用软件实现PID控制,即数字PID控制。
数字式PID控制算法可以分为位置式PID和增量式PID控制算法。
2位置式PID算法
由于计算机控制是一种采样控制,它只能根据采样时刻的偏差计算控制量,而不能像模拟控制那样连续输出控制量量,进行连续控制。由于这一特点,式2中的积分项和微分项不能直接使用,必须进行离散化处理。离散化处理的方法为:以T作为采样周期,k作为采样序号,则离散采样时间kT对应着连续时间t,用矩形法数值积分近似代替积分,用一阶后向差分近似代替微分,可作如下近似变换:
上式中,为了表示的方便,将类似于e(kT)简化成ek等。
将式3代入式2,就可以得到离散的PID表达式为:
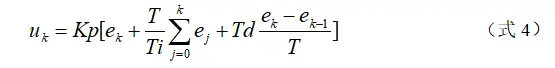
或:
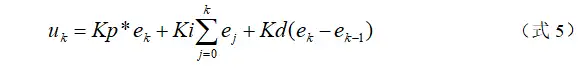
其中,k为采样序号,k=0,1,2,……;
uk为第次采样时刻的计算机输出值;
ek为第次采样时刻输入的偏差值;
ek-1为第k-1次采样时刻输入的偏差值;
Ki为积分系数,Ki=Kp*T/Ti;
为微分系数,Kd=Kp*Td/T;
如果采样周期足够小,则式4或式5的近似计算可以获得足够精确的结果,离散控制过程与连续过程十分接近。
式4或式5表示的控制算法直接按式2所给出的PID控制规律定义进行计算的,所以它给出了全部控制量的大小,因此被称为全量式或位置式PID控制算法。
这种算法的缺点是:由于全量输出,所以每次输出均与过去状态有关,计算时要对ek进行累加,工作量大;并且,因为计算机输出的uk对应的是执行机构的实际位置,如果计算机出现故障,输出的uk将大幅度变化,会引起执行机构的大幅度变化,有可能因此造成严重的生产事故,这在实生产际中是不允许的。
增量式PID控制算法可以避免这种现象发生。
3增量式PID算法
所谓增量式PID是指数字控制器的输出只是控制量的增量Δuk。当执行机构需要的控制量是增量,而不是位置量的绝对数值时,可以使用增量式PID控制算法进行控制。
增量式PID控制算法可以通过式4推导出。由式4可以得到控制器的第k-1个采样时刻的输出值为:
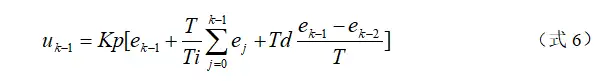
将式4与6相减并整理,就可以得到增量式PID控制算法公式为:
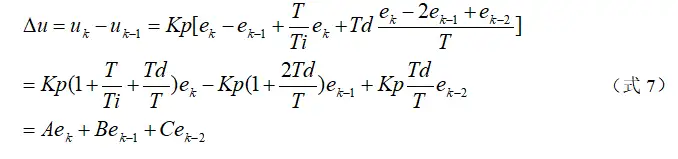
其中:
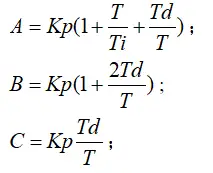
由式7可以看出,如果计算机控制系统采用恒定的采样周期T,一旦确定A、B、C,只要使用前后三次测量的偏差值,就可以由7求出控制量。
增量式PID控制算法与位置式PID算法(如式4)相比,计算量小的多,因此在实际中得到广泛的应用。
而位置式PID控制算法也可以通过增量式控制算法推出递推计算公式:

式8就是目前在计算机控制中广泛应用的数字递推PID控制算法。
4控制器参数整定
控制器参数整定:指决定调节器的比例系数Kp、积分时间Ti、微分时间Td和采样周期Ts的具体数值。整定的实质是通过改变调节器的参数,使其特性和过程特性相匹配,以改善系统的动态和静态指标,取得最佳的控制效果。
整定调节器参数的方法很多,归纳起来可分为两大类,即理论计算整定法和工程整定法。理论计算整定法有对数频率特性法和根轨迹法等;工程整定法有凑试法、临界比例法、经验法、衰减曲线法和响应曲线法等。工程整定法特点不需要事先知道过程的数学模型,直接在过程控制系统中进行现场整定,方法简单、计算简便、易于掌握。
凑试法
按照先比例(P)、再积分(I)、最后微分(D)的顺序。
置调节器积分时间Ti=∞,微分时间Td=0,在比例系数按经验设置的初值条件下,将系统投入运行,由小到大整定比例系数Kp。求得满意的1/4衰减度过渡过程曲线。
引入积分作用(此时应将上述比例系数Kp设置为5/6Kp)。将Ti由大到小进行整定。
若需引入微分作用时,则将Td按经验值或按Td=(1/3~1/4)Ti设置,并由小到大加入。
临界比例法
在闭环控制系统里,将调节器置于纯比例作用下,从小到大逐渐改变调节器的比例系数,得到等幅振荡的过渡过程。此时的比例系数称为临界比例系数Ku,相邻两个波峰间的时间间隔,称为临界振荡周期Tu。
临界比例度法步骤:
1、将调节器的积分时间Ti置于最大(Ti=∞),微分时间置零(Td=0),比例系数Kp适当,平衡操作一段时间,把系统投入自动运行。
2、将比例系数Kp逐渐增大,得到等幅振荡过程,记下临界比例系数Ku和临界振荡周期Tu值。
3、根据Ku和Tu值,采用经验公式,计算出调节器各个参数,即Kp、Ti和Td的值。
按“先P再I最后D”的操作程序将调节器整定参数调到计算值上。若还不够满意,可再作进一步调整。
临界比例度法整定注意事项:
有的过程控制系统,临界比例系数很大,使系统接近两式控制,调节阀不是全关就是全开,对工业生产不利。
有的过程控制系统,当调节器比例系数Kp调到最大刻度值时,系统仍不产生等幅振荡,对此,就把最大刻度的比例度作为临界比例度Ku进行调节器参数整定。
经验法
用凑试法确定PID参数需要经过多次反复的实验,为了减少凑试次数,提高工作效率,可以借鉴他人的经验,并根据一定的要求,事先作少量的实验,以得到若干基准参数,然后按照经验公式,用这些基准参数导出PID控制参数,这就是经验法。
临界比例法就是一种经验法。这种方法首先将控制器选为纯比例控制器,并形成闭环,改变比例系数,使系统对阶跃输入的响应达到临界状态,这时记下比例系数Ku、临界振荡周期为Tu,根据Z-N提供的经验公式,就可以由这两个基准参数得到不同类型控制器的参数,如表1所示。
表1 临界比例法确定的模拟控制器参数
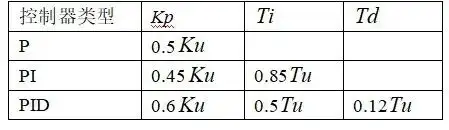
这种临界比例法是针对模拟PID控制器,对于数字PID控制器,只要采样周期取的较小,原则上也同样使用。在电动机的控制中,可以先采用临界比例法,然后在采用临界比例法求得结果的基础上,用凑试法进一步完善。
表1的控制参数,实际上是按衰减度为1/4时得到的。通常认为1/4的衰减度能兼顾到稳定性和快速性。如果要求更大的衰减,则必须用凑试法对参数作进一步的调整。
采样周期的选择
Shannon采样定律:为不失真地复现信号的变化,采样频率至少应大于或等于连续信号最高频率分量的二倍。根据采样定律可以确定采样周期的上限值。实际采样周期的选择还要受到多方面因素的影响,不同的系统采样周期应根据具体情况来选择。
采样周期的选择,通常按照过程特性与干扰大小适当来选取采样周期:即对于响应快、(如流量、压力)波动大、易受干扰的过程,应选取较短的采样周期;反之,当过程响应慢(如温度、成份)、滞后大时,可选取较长的采样周期。
采样周期的选取应与PID参数的整定进行综合考虑,采样周期应远小于过程的扰动信号的周期,在执行器的响应速度比较慢时,过小的采样周期将失去意义,因此可适当选大一点;在计算机运算速度允许的条件下,采样周期短,则控制品质好;当过程的纯滞后时间较长时,一般选取采样周期为纯滞后时间的1/4~1/8。
5参数调整规则探索
人们通过对PID控制理论的认识和长期人工操作经验的总结,可知PID参数应依据以下几点来适应系统的动态过程。
1、在偏差比较大时,为使尽快消除偏差,提高响应速度,同时为了避免系统响应出现超调,Kp取大值,Ki取零;在偏差比较小时,为继续减小偏差,并防止超调过大、产生振荡、稳定性变坏,Kp值要减小,Ki取小值;在偏差很小时,为消除静差,克服超调,使系统尽快稳定,Kp值继续减小,Ki值不变或稍取大。
2、当偏差与偏差变化率同号时,被控量是朝偏离既定值方向变化。因此,当被控量接近定值时,反号的比列作用阻碍积分作用,避免积分超调及随之而来的振荡,有利于控制;而当被控量远未接近各定值并向定值变化时,则由于这两项反向,将会减慢控制过程。在偏差比较大时,偏差变化率与偏差异号时,Kp值取零或负值,以加快控制的动态过程。
3、偏差变化率的大小表明偏差变化的速率,ek-ek-1越大,Kp取值越小,Ki取值越大,反之亦然。同时,要结合偏差大小来考虑。
4、微分作用可改善系统的动态特性,阻止偏差的变化,有助于减小超调量,消除振荡,缩短调节时间ts,允许加大Kp,使系统稳态误差减小,提高控制精度,达到满意的控制效果。所以,在ek比较大时,Kd取零,实际为PI控制;在ek比较小时,Kd取一正值,实行PID控制。
审核编辑 黄宇